### 2021.12.24
나이브 베이스 분류기(Naive Bayes Classification)
- 베이즈 정리를 적용한 확률적 분류 알고리즘
- 모든 특성들이 독립임을 가정 (naive 가정)
- 입력 특성에 따라 3개의 분류기 존재
- 가우시안 나이브 베이즈 분류기
- 베르누이 나이브 베이즈 분류기
- 다항 나이브 베이즈 분류기
나이브 베이즈 분류기의 확률 모델

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.naive_bayes import GaussianNB, BernoulliNB, MultinomialNB
from sklearn.datasets import fetch_covtype, fetch_20newsgroups
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler, MinMaxScaler
from sklearn.feature_extraction.text import CountVectorizer, HashingVectorizer, TfidfVectorizer
from sklearn import metrics#In[]
#나이브 베이스 기본 동작 모형
prior = [0.45, 0.3, 0.15, 0.1] #발생확률 가정
likelihood = [[0.3, 0.3, 0.4], [0.7, 0.2, 0.1], [0.15, 0.5, 0.35], [0.6,0.2,0.2]]
idx = 0
for c, xs in zip(prior, likelihood):
result = 1.
for x in xs :
result *= x
result *= c
idx += 1
print(f"{idx}번째 클래스의 가능성 : {result}")
#Out[]
1번째 클래스의 가능성 : 0.0162
2번째 클래스의 가능성 : 0.0042
3번째 클래스의 가능성 : 0.0039375
4번째 클래스의 가능성 : 0.0024000000000000002
1. 산림 토양 데이터
- 산림 지역 토양의 특징 데이터
- 토양이 어떤 종류에 속하는지 예측
- https://archive.ics.uci.edu/ml/datasets/Covertype 에서 데이터의 자세한 설명 확인 가능
#In[]
covtype = fetch_covtype()
print(covtype.DESCR)
#Out[]
.. _covtype_dataset:
Forest covertypes
-----------------
The samples in this dataset correspond to 30×30m patches of forest in the US,
collected for the task of predicting each patch's cover type,
i.e. the dominant species of tree.
There are seven covertypes, making this a multiclass classification problem.
Each sample has 54 features, described on the
`dataset's homepage <https://archive.ics.uci.edu/ml/datasets/Covertype>`__.
Some of the features are boolean indicators,
while others are discrete or continuous measurements.
**Data Set Characteristics:**
================= ============
Classes 7
Samples total 581012
Dimensionality 54
Features int
================= ============
:func:`sklearn.datasets.fetch_covtype` will load the covertype dataset;
it returns a dictionary-like 'Bunch' object
with the feature matrix in the ``data`` member
and the target values in ``target``. If optional argument 'as_frame' is
set to 'True', it will return ``data`` and ``target`` as pandas
data frame, and there will be an additional member ``frame`` as well.
The dataset will be downloaded from the web if necessary.#In[]
pd.DataFrame(covtype.data)
#Out[]
#In[]
covtype.target
#Out[]
array([5, 5, 2, ..., 3, 3, 3], dtype=int32)
1-1. 학습, 평가 데이터 분류
#In[]
covtype_X = covtype.data
covtype_y = covtype.target
covtype_X_train, covtype_X_test, covtype_y_train, covtype_y_test = train_test_split(covtype_X, covtype_y, test_size=0.2)
print("전체 데이터 크기 : {}".format(covtype_X.shape))
print("학습 데이터 크기 : {}".format(covtype_X_train.shape))
print("평가 데이터 크기 : {}".format(covtype_X_test.shape))
#Out[]
전체 데이터 크기 : (581012, 54)
학습 데이터 크기 : (464809, 54)
평가 데이터 크기 : (116203, 54)
1-2. 전처리
전치리 전 데이터
#In[]
covtype_df = pd.DataFrame(data=covtype_X)
covtype_df.describe()
#Out[]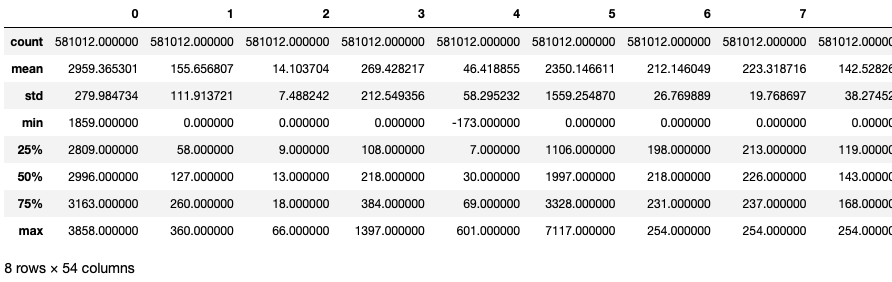
#In[]
covtype_train_df = pd.DataFrame(data=covtype_X_train)
covtype_train_df.describe()
#Out[]
#In[]
covtype_test_df = pd.DataFrame(data=covtype_X_test)
covtype_test_df.describe()
#Out[]
전처리 과정
- 평균은 0에 가깝게, 표준평차는 1에 가깝게 정규화
#In[]
scaler = StandardScaler()
covtype_X_train_scale = scaler.fit_transform(covtype_X_train)
covtype_X_test_scale = scaler.transform(covtype_X_test)
전처리 후 데이터
#In[]
covtype_train_df = pd.DataFrame(data=covtype_X_train_scale)
covtype_train_df.describe()
#Out[]
#In[]
covtype_test_df = pd.DataFrame(data=covtype_X_test_scale)
covtype_test_df.describe()
#Out[]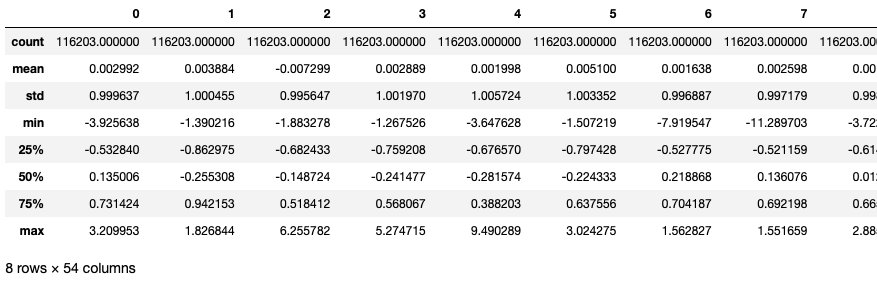
2. 20 Newsgroup 데이터
- 뉴스 기사가 어느 그룹에 속하는지 분류
- 뉴스 기사는 텍스트 데이터이기 때문에 특별한 전처리 과정이 필요
#In[]
newsgroup = fetch_20newsgroups()
print(newsgroup.DESCR)
#Out[]
생략!!#In[]
newsgroup.target_names
#Out[]
['alt.atheism',
'comp.graphics',
'comp.os.ms-windows.misc',
'comp.sys.ibm.pc.hardware',
'comp.sys.mac.hardware',
'comp.windows.x',
'misc.forsale',
'rec.autos',
'rec.motorcycles',
'rec.sport.baseball',
'rec.sport.hockey',
'sci.crypt',
'sci.electronics',
'sci.med',
'sci.space',
'soc.religion.christian',
'talk.politics.guns',
'talk.politics.mideast',
'talk.politics.misc',
'talk.religion.misc']
2-1. 학습, 평가 데이터 분류
#In[]
newsgroup_train = fetch_20newsgroups(subset='train')
newsgroup_test = fetch_20newsgroups(subset='test')
X_train, y_train = newsgroup_train.data, newsgroup_train.target
X_test, y_test = newsgroup_test.data, newsgroup_test.target
2-2. 벡터화
- 텍스트 데이터는 기계학습 모델에 입력 할 수 없음
- 벡터화는 텍스트 데이터를 실수 벡터로 변환해 기계학습 모델에 입력 할 수 있도록 하는 전처리 과정
- Scikit-learn에서는 Count, Tf-idf, Hashing 세가지 방법을 지원
2-2-1. CountVectorizer
- 문서에 나온 단어의 수를 세서 벡터 생성
#In[]
count_vectorizer = CountVectorizer()
X_train_count = count_vectorizer.fit_transform(X_train)
X_test_count = count_vectorizer.transform(X_test)데이터를 희소 행렬 형태로 표현
#In[]
X_train_count
#Out[]
<11314x130107 sparse matrix of type '<class 'numpy.int64'>'
with 1787565 stored elements in Compressed Sparse Row format>#In[]
for v in X_train_count[0]:
print(v)
#Out[]
(0, 56979) 3
(0, 75358) 2
(0, 123162) 2
(0, 118280) 2
(0, 50527) 2
(0, 124031) 2
(0, 85354) 1
(0, 114688) 1
(0, 111322) 1
(0, 123984) 1
(0, 37780) 5
(0, 68532) 3
(0, 114731) 5
(0, 87620) 1
(0, 95162) 1
(0, 64095) 1
(0, 98949) 1
(0, 90379) 1
(0, 118983) 1
(0, 89362) 3
(0, 79666) 1
(0, 40998) 1
(0, 92081) 1
(0, 76032) 1
(0, 4605) 1
: :
(0, 37565) 1
(0, 113986) 1
(0, 83256) 1
(0, 86001) 1
(0, 51730) 1
(0, 109271) 1
(0, 128026) 1
(0, 96144) 1
(0, 78784) 1
(0, 63363) 1
(0, 90252) 1
(0, 123989) 1
(0, 67156) 1
(0, 128402) 2
(0, 62221) 1
(0, 57308) 1
(0, 76722) 1
(0, 94362) 1
(0, 78955) 1
(0, 114428) 1
(0, 66098) 1
(0, 35187) 1
(0, 35983) 1
(0, 128420) 1
(0, 86580) 1
2-2-2. HashingVectorizer
- 각 단어를 해쉬 값으로 표현
- 미리 정해진 크기의 벡터로 표현
#In[]
hash_vectorizer = HashingVectorizer(n_features=1000) #1000개로 제한
X_train_hash = hash_vectorizer.fit_transform(X_train)
X_test_hash = hash_vectorizer.transform(X_test)
X_train_hash
#Out[]
<11314x1000 sparse matrix of type '<class 'numpy.float64'>'
with 1550687 stored elements in Compressed Sparse Row format>#In[]
print(X_train_hash[0])
#Out[]
(0, 80) -0.0642824346533225
(0, 108) 0.0642824346533225
(0, 111) -0.128564869306645
(0, 145) 0.0642824346533225
(0, 158) 0.0642824346533225
(0, 159) -0.0642824346533225
(0, 161) 0.0642824346533225
(0, 165) -0.0642824346533225
(0, 171) 0.0642824346533225
(0, 182) 0.0642824346533225
(0, 195) -0.0642824346533225
(0, 196) 0.19284730395996752
(0, 205) -0.0642824346533225
(0, 209) 0.0642824346533225
(0, 234) 0.0642824346533225
(0, 237) 0.0642824346533225
(0, 248) 0.0642824346533225
(0, 265) 0.19284730395996752
(0, 274) 0.0642824346533225
(0, 277) 0.19284730395996752
(0, 284) -0.0642824346533225
(0, 286) -0.0642824346533225
(0, 296) 0.0642824346533225
(0, 362) -0.0642824346533225
(0, 364) -0.0642824346533225
: :
(0, 739) 0.0
(0, 761) -0.0642824346533225
(0, 766) 0.0642824346533225
(0, 800) -0.0642824346533225
(0, 812) -0.0642824346533225
(0, 842) 0.0642824346533225
(0, 848) -0.0642824346533225
(0, 851) 0.0642824346533225
(0, 863) -0.0642824346533225
(0, 881) 0.0642824346533225
(0, 892) 0.0642824346533225
(0, 897) 0.0
(0, 899) 0.0642824346533225
(0, 906) -0.0642824346533225
(0, 918) 0.128564869306645
(0, 926) -0.0642824346533225
(0, 935) 0.0642824346533225
(0, 939) -0.0642824346533225
(0, 951) -0.0642824346533225
(0, 958) -0.38569460791993504
(0, 960) 0.0642824346533225
(0, 968) -0.0642824346533225
(0, 987) -0.0642824346533225
(0, 996) 0.0642824346533225
(0, 997) -0.128564869306645
2-2-3. TfidfVectorizer

#In[]
tfidf_vectorizer = TfidfVectorizer()
X_train_tfidf = tfidf_vectorizer.fit_transform(X_train)
X_test_tfidf = tfidf_vectorizer.transform(X_test)
X_train_tfidf
#Out[]
<11314x130107 sparse matrix of type '<class 'numpy.float64'>'
with 1787565 stored elements in Compressed Sparse Row format>#In[]
for v in X_train_tfidf[0]:
print(v)
#Out[]
(0, 86580) 0.13157118714240987
(0, 128420) 0.04278499079283093
(0, 35983) 0.03770448563619875
(0, 35187) 0.09353930598317124
(0, 66098) 0.09785515708314481
(0, 114428) 0.05511105154696676
(0, 78955) 0.05989856888061599
(0, 94362) 0.055457031390147224
(0, 76722) 0.06908779999621749
(0, 57308) 0.1558717009157704
(0, 62221) 0.02921527992427867
(0, 128402) 0.05922294083277842
(0, 67156) 0.07313443922740179
(0, 123989) 0.08207027465330353
(0, 90252) 0.031889368795417566
(0, 63363) 0.08342748387969037
(0, 78784) 0.0633940918806495
(0, 96144) 0.10826904490745741
(0, 128026) 0.060622095889758885
(0, 109271) 0.10844724822064673
(0, 51730) 0.09714744057976722
(0, 86001) 0.07000411445838192
(0, 83256) 0.08844382496462173
(0, 113986) 0.17691750674853082
(0, 37565) 0.03431760442478462
: :
(0, 4605) 0.06332603952480323
(0, 76032) 0.019219463052223086
(0, 92081) 0.09913274493911223
(0, 40998) 0.0780136819691811
(0, 79666) 0.10936401252414274
(0, 89362) 0.06521174306303763
(0, 118983) 0.037085978050619146
(0, 90379) 0.019928859956645867
(0, 98949) 0.16068606055394932
(0, 64095) 0.03542092427131355
(0, 95162) 0.03447138409326312
(0, 87620) 0.035671863140815795
(0, 114731) 0.14447275512784058
(0, 68532) 0.07325812342131596
(0, 37780) 0.38133891259493113
(0, 123984) 0.036854292634593756
(0, 111322) 0.01915671802495043
(0, 114688) 0.06214070986309586
(0, 85354) 0.03696978508816316
(0, 124031) 0.10798795154169122
(0, 50527) 0.054614286588587246
(0, 118280) 0.2118680720828169
(0, 123162) 0.2597090245735688
(0, 75358) 0.35383501349706165
(0, 56979) 0.057470154074851294
3. 가우시안 나이브 베이즈
- 입력 특성이 가우시안(정규) 분포를 갖는다고 가정
#In[]
model = GaussianNB()
model.fit(covtype_X_train_scale, covtype_y_train)
#Out[]
GaussianNB()train data score
#In[]
predict = model.predict(covtype_X_train_scale)
acc = metrics.accuracy_score(covtype_y_train, predict)
f1 = metrics.f1_score(covtype_y_train, predict, average=None)
print("Train Accuracy: {}".format(acc))
print("Train F1 score : {}".format(f1))
#Out[]
Train Accuracy: 0.08788771301760508
Train F1 score : [0.03981986 0.01766797 0.33531383 0.13789636 0.04358284 0.07112195
0.23669609]test data score
#In[]
predict = model.predict(covtype_X_test_scale)
acc = metrics.accuracy_score(covtype_y_test, predict)
f1 = metrics.f1_score(covtype_y_test, predict, average=None)
print("Test Accuracy: {}".format(acc))
print("Test F1 score : {}".format(f1))
#Out[]
Test Accuracy: 0.0884486631154101
Test F1 score : [0.04288833 0.01908018 0.33367329 0.14015968 0.04165637 0.0736687
0.23903186]시각화
#In[]
from sklearn.datasets import make_blobs
def make_meshgrid(x,y,h=.02):
x_min, x_max = x.min()-1, x.max()+1
y_min, y_max = y.min()-1, y.max()+1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
return xx, yy
def plot_contours(clf, xx, yy, **params):
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
out = plt.contourf(xx, yy, Z, **params)
return out#In[]
X, y = make_blobs(n_samples=1000)
plt.scatter(X[:,0], X[:, 1], c=y, cmap=plt.cm.coolwarm, s=20, edgecolors='k')
#Out[]
#In[1]
model = GaussianNB()
model.fit(X,y)
#Out[1]
GaussianNB()
#In[2]
xx, yy = make_meshgrid(X[:,0], X[:, 1])
plot_contours(model, xx, yy, cmap=plt.cm.coolwarm, alpha=0.8)
plt.scatter(X[:,0], X[:, 1], c=y, cmap=plt.cm.coolwarm, s=20, edgecolors='k')
#Out[2]
4. 베르누이 나이브 베이즈
- 입력 특성이 베르누이 분포에 의해 생성된 이진 값을 갖는 다고 가정
4-1. 학습 및 평가 (Count)
#In[]
model = BernoulliNB()
model.fit(X_train_count, y_train)
#Out[]
BernoulliNB()
#In[]
predict = model.predict(X_train_count)
acc = metrics.accuracy_score(y_train, predict)
f1 = metrics.f1_score(y_train, predict, average=None)
print('Train Accauracy : {}'.format(acc))
print('Train F1 Score : {}'.format(f1))
#Out[]
Train Accauracy : 0.7821283365741559
Train F1 Score : [0.80096502 0.8538398 0.13858268 0.70686337 0.85220126 0.87944493
0.51627694 0.84532672 0.89064976 0.87179487 0.94561404 0.91331546
0.84627832 0.89825848 0.9047619 0.79242424 0.84693878 0.84489796
0.67329545 0.14742015]#In[]
predict = model.predict(X_test_count)
acc = metrics.accuracy_score(y_test, predict)
f1 = metrics.f1_score(y_test, predict, average=None)
print('Test Accauracy : {}'.format(acc))
print('Test F1 Score : {}'.format(f1))
#Out[]
Test Accauracy : 0.6307753584705258
Test F1 Score : [0.47086247 0.60643564 0.01 0.56014047 0.6953405 0.70381232
0.44829721 0.71878646 0.81797753 0.81893491 0.90287278 0.74794521
0.61647059 0.64174455 0.76967096 0.63555114 0.64285714 0.77971474
0.31382979 0.00793651]
4-2. 학습 및 평가 (Hash)
#In[]
model = BernoulliNB()
model.fit(X_train_hash, y_train)
#Out[]
BernoulliNB()#In[]
predict = model.predict(X_train_hash)
acc = metrics.accuracy_score(y_train, predict)
f1 = metrics.f1_score(y_train, predict, average=None)
print('Train Accauracy : {}'.format(acc))
print('Train F1 Score : {}'.format(f1))
#Out[]
Train Accauracy : 0.5951917977726711
Train F1 Score : [0.74226804 0.49415205 0.45039019 0.59878155 0.57327935 0.63929619
0.35390947 0.59851301 0.72695347 0.68123862 0.79809524 0.70532319
0.54703833 0.66862745 0.61889927 0.74707471 0.6518668 0.60485269
0.5324165 0.54576271]#In[]
predict = model.predict(X_test_hash)
acc = metrics.accuracy_score(y_test, predict)
f1 = metrics.f1_score(y_test, predict, average=None)
print('Test Accauracy : {}'.format(acc))
print('Test F1 Score : {}'.format(f1))
#Out[]
Test Accauracy : 0.4430430164630908
Test F1 Score : [0.46678636 0.33826638 0.29391892 0.45743329 0.41939121 0.46540881
0.34440068 0.46464646 0.62849873 0.53038674 0.63782051 0.55251799
0.32635983 0.34266886 0.46105919 0.61780105 0.46197991 0.54591837
0.27513228 0.3307888 ]
4-3. 학습 및 평가 (Tf-idf)
#In[]
model = BernoulliNB()
model.fit(X_train_tfidf, y_train)
#Out[]
BernoulliNB()#In[]
predict = model.predict(X_train_tfidf)
acc = metrics.accuracy_score(y_train, predict)
f1 = metrics.f1_score(y_train, predict, average=None)
print('Train Accauracy : {}'.format(acc))
print('Train F1 Score : {}'.format(f1))
#Out[]
Train Accauracy : 0.7821283365741559
Train F1 Score : [0.80096502 0.8538398 0.13858268 0.70686337 0.85220126 0.87944493
0.51627694 0.84532672 0.89064976 0.87179487 0.94561404 0.91331546
0.84627832 0.89825848 0.9047619 0.79242424 0.84693878 0.84489796
0.67329545 0.14742015]#In[]
predict = model.predict(X_test_tfidf)
acc = metrics.accuracy_score(y_test, predict)
f1 = metrics.f1_score(y_test, predict, average=None)
print('Test Accauracy : {}'.format(acc))
print('Test F1 Score : {}'.format(f1))
#Out[]
Test Accauracy : 0.6307753584705258
Test F1 Score : [0.47086247 0.60643564 0.01 0.56014047 0.6953405 0.70381232
0.44829721 0.71878646 0.81797753 0.81893491 0.90287278 0.74794521
0.61647059 0.64174455 0.76967096 0.63555114 0.64285714 0.77971474
0.31382979 0.00793651]
4-4. 시각화
#In[]
X, y = make_blobs(n_samples=1000)
plt.scatter(X[:,0], X[:, 1], c=y, cmap=plt.cm.coolwarm, s=20, edgecolors='k')
#Out[]
#In[1]
model = BernoulliNB()
model.fit(X,y)
#Out[1]
BernoulliNB()
#In[2]
xx, yy = make_meshgrid(X[:,0], X[:, 1])
plot_contours(model, xx, yy, cmap=plt.cm.coolwarm, alpha=0.8)
plt.scatter(X[:,0], X[:, 1], c=y, cmap=plt.cm.coolwarm, s=20, edgecolors='k')
#Out[2]
5. 다항 나이브 베이즈
- 입력 특성이 다항분포에 의해 생성된 빈도수 값을 갖는 다고 가정
5-1. 학습 및 평가 (Count)
#In[]
model = MultinomialNB()
model.fit(X_train_count, y_train)
#Out[]
MultinomialNB()#In[]
predict = model.predict(X_train_count)
acc = metrics.accuracy_score(y_train, predict)
f1 = metrics.f1_score(y_train, predict, average=None)
print('Train Accauracy : {}'.format(acc))
print('Train F1 Score : {}'.format(f1))
#Out[]
Train Accauracy : 0.9245182959165635
Train F1 Score : [0.95228426 0.904 0.25073746 0.81402003 0.96669513 0.88350983
0.90710383 0.97014925 0.98567818 0.99325464 0.98423237 0.95399516
0.95703454 0.98319328 0.98584513 0.95352564 0.97307002 0.97467249
0.95157895 0.86526946]#In[]
predict = model.predict(X_test_count)
acc = metrics.accuracy_score(y_test, predict)
f1 = metrics.f1_score(y_test, predict, average=None)
print('Test Accauracy : {}'.format(acc))
print('Test F1 Score : {}'.format(f1))
#Out[]
Test Accauracy : 0.7728359001593202
Test F1 Score : [0.77901431 0.7008547 0.00501253 0.64516129 0.79178082 0.73370166
0.76550681 0.88779285 0.93951094 0.91390728 0.94594595 0.78459938
0.72299169 0.84635417 0.86029412 0.80846561 0.78665077 0.89281211
0.60465116 0.48695652]
5-2. 학습 및 평가 (Tf-idf)
#In[]
model = MultinomialNB()
model.fit(X_train_tfidf, y_train)
#Out[]
MultinomialNB()#In[]
predict = model.predict(X_train_tfidf)
acc = metrics.accuracy_score(y_train, predict)
f1 = metrics.f1_score(y_train, predict, average=None)
print('Train Accauracy : {}'.format(acc))
print('Train F1 Score : {}'.format(f1))
#Out[]
Train Accauracy : 0.9326498143892522
Train F1 Score : [0.87404162 0.95414462 0.95726496 0.92863002 0.97812773 0.97440273
0.91090909 0.97261411 0.98659966 0.98575021 0.98026316 0.94033413
0.9594478 0.98032506 0.97755611 0.77411003 0.93506494 0.97453907
0.90163934 0.45081967]#In[]
predict = model.predict(X_test_tfidf)
acc = metrics.accuracy_score(y_test, predict)
f1 = metrics.f1_score(y_test, predict, average=None)
print('Test Accauracy : {}'.format(acc))
print('Test F1 Score : {}'.format(f1))
#Out[]
Test Accauracy : 0.7738980350504514
Test F1 Score : [0.63117871 0.72 0.72778561 0.72104019 0.81309686 0.81643836
0.7958884 0.88135593 0.93450882 0.91071429 0.92917167 0.73583093
0.69732938 0.81907433 0.86559803 0.60728118 0.76286353 0.92225201
0.57977528 0.24390244]
5-3. 시각화
#In[]
X, y = make_blobs(n_samples=1000)
scaler = MinMaxScaler()
X = scaler.fit_transform(X)
plt.scatter(X[:,0], X[:, 1], c=y, cmap=plt.cm.coolwarm, s=20, edgecolors='k')
#Out[]
#In[1]
model = MultinomialNB()
model.fit(X, y)
#Out[1]
MultinomialNB()
#In[2]
xx, yy = make_meshgrid(X[:,0], X[:, 1])
plot_contours(model, xx, yy, cmap=plt.cm.coolwarm, alpha=0.8)
plt.scatter(X[:,0], X[:, 1], c=y, cmap=plt.cm.coolwarm, s=20, edgecolors='k')
#Out[2]
'Youtube > 머신러닝' 카테고리의 다른 글
| [머신러닝] #6 최근접 이웃(K Nearest Neighbor) (0) | 2021.12.27 |
|---|---|
| [머신러닝] #5 서포트 벡터 머신 (0) | 2021.12.22 |
| [머신러닝] #4 로지스틱회귀 (0) | 2021.12.21 |
| [머신러닝] #3 선형 모델 Linear Models (0) | 2021.12.20 |
| [머신러닝] #2 Scikits-learn (0) | 2021.12.20 |